NTT(快速数论变换)
1 算法介绍
1.1 多项式乘法引入
1.1.1 多项式的两种表示方法
一般 $n$ 次多项式如公式(1)所示。多项式具有两种表示方法分别是系数表示法和点值表示法。
$$
\begin{equation}
A(x)=a_0+a_1x^1+a_2x^2+\ldots +a_{n-1}x^{n-1}+a_nx^n=\sum^{n}_{i=0}a_ix^i
\end{equation}
$$
系数表示法:
任意多项式都可以通过一组系数所确定,而这组系数所组成的向量也叫做系数向量,通过系数向量表示一个多项的方式也叫做系数表示法。例如公式(1)中 $A(x)$ 的系数向量为:$\mathbf{a}=[a_0 ,a_1,\ldots,a_{n-1},a_n]$。
点值表示法:
对于一个已知的多项式例如公式(1)中的 $A(x)$ ,将 $x_i$ 代进去可以得到一个确定的值 $y_i$ ,如:$y_0=A(x_0)$ 。且可将 $(x_0,y_0)$ 看作是坐标系上的一个点。可将任意多(互不相等)的自变量 $( x_1,x_2,\ldots,x_{n-1}, x_n)$ 代入到 $A(x)$ 中,从而得到更多的点:$(x_1,y_1),(x_2,y_2),\ldots(x_n,y_n)$。通过 n+1 个不同点组成的点集 $P={(x_0,y_0),(x_1,y_1),\ldots,(x_n,y_n)} $ ,唯一确定一个 n 次多项式,该方式也叫做多项式的点值表示法。
1.1.2 多项式乘法
已知两个多项式 $A(x)$ 和 $B(x)$,分别是 $n$ 次多项式和 m 次多项式。
$$
\begin{align}
A(x)=\sum^{n}_{i=0}a_ix^i\\
B(x)=\sum^{m}_{i=0}b_ix^i
\end{align}
$$
公式(2)和公式(3)相乘得到一个最高为 $n+m$ 次的多项式 $C(x)$。系数向量:$\mathbf{c}=[c_0 ,c_1,\ldots,c_{m+n}]$。
$$
\begin{align}
C(x)=\sum^{n+m}_{i=0}c_ix^i
\end{align}
$$
系数乘法:
系数乘法,将两个多项式的系数相乘,系数相乘,如公式(5)所示。不难看出时间复杂为 $O(n^2)$。整理可得公式(6)。
$$
\begin{align}
C_{i+j}= \sum_{i=0}^{n} \sum_{j=0}^{m} a_i b_j
\end{align}
$$
$$
\begin{align}
C_i=\sum^{i}_{j=0}a_jb_{i-j}
\end{align}
$$
点值乘法:
点值乘法只需将要将对应的纵坐标相乘即可,但是因为新得到的多项式次数更高,所以每个因子多项式都需要提供 $m+n+1$ 个点参与运算。时间复杂度为 $O(n)$。
小结
在计算多项式乘法时,点值表示的时间复杂度低。但是在计算系统中系数表示更加的常用。于是很自然的想到,在进行乘法时从系数表示转换到点值表示,使用点值表示法进行乘法运算,然后再转换为系数表示法。
但是很不幸的是,从系数表示转换到点值表示,以及点值表示到系数表示,这两个过程的时间复杂度均为 $O(n^2)$。
图1 多项式乘法总结图
1.1.3 转换优化
如果通过减少求值的点数可以较少计算时间。根据函数的奇偶性我们可以只求一半的点值,从而减少一半的计算量。这里为了方便表示设一个 $n-1$ 次的一般多项式,$n=2^a , a\in \N$。
$$
P(x)=p_0+p_1x^1+p_2x^2+\ldots +p_{n-1}x^{n-1}=\sum^{n-1}_{i=0}p_ix^i
$$
将偶次项和奇数项分别组合:
$$
P(x)=(p_0+p_2x^2\ldots+p_{n-2}x^{n-2})+(p_1x^1+\ldots +p_{n-1}x^{n-1})
$$
对奇次项提取公因式 $x$:
$$
P(x)=(p_0+p_2x^2\ldots+p_{n-2}x^{n-2})+x(p_1x^0+\ldots +p_{n-1}x^{n-2})
$$
化简为:
$$
\begin{align}
P(x)=P_e(x^2)+xP_o(x^2)
\end{align}
$$
则我们可以取 $\frac{n}{2}$ 对相反数点,这样我们只需要计算一半的点值。
$$
P(x_i)=P_e(x_i^2)+xP_o(x_i^2) \\
P(-x_i)=P_e(x_i^2)-x_iP_o(x_i^2)
$$
观察公式(7)不难发现,是将是将 $P(x)$ 拆成了两个规模为 $\frac{n}{2}$ 的 $P_e(x)$,$P_o(x)$。自然而然想到了递归执行。但是问题是相反数平方运算后所得结果均为正数,无法构造相反数对,无法实现递归。如果能一直保持相反数点对,那么时间复杂度可以表示为 $T$ $($**$n$$)$ $=$$T$ $($$2$ $n)$$+$ $O$$($ $n$**$)$,即时间复杂度为 $O(n\log n)$。
1.1.4 单位根(复平面)
既然实数域没有办法解决上面的问题,可以将起扩展到复平面。我们希望取一些点使其平方后的结果依然存在相反数对。
图2 复平面图
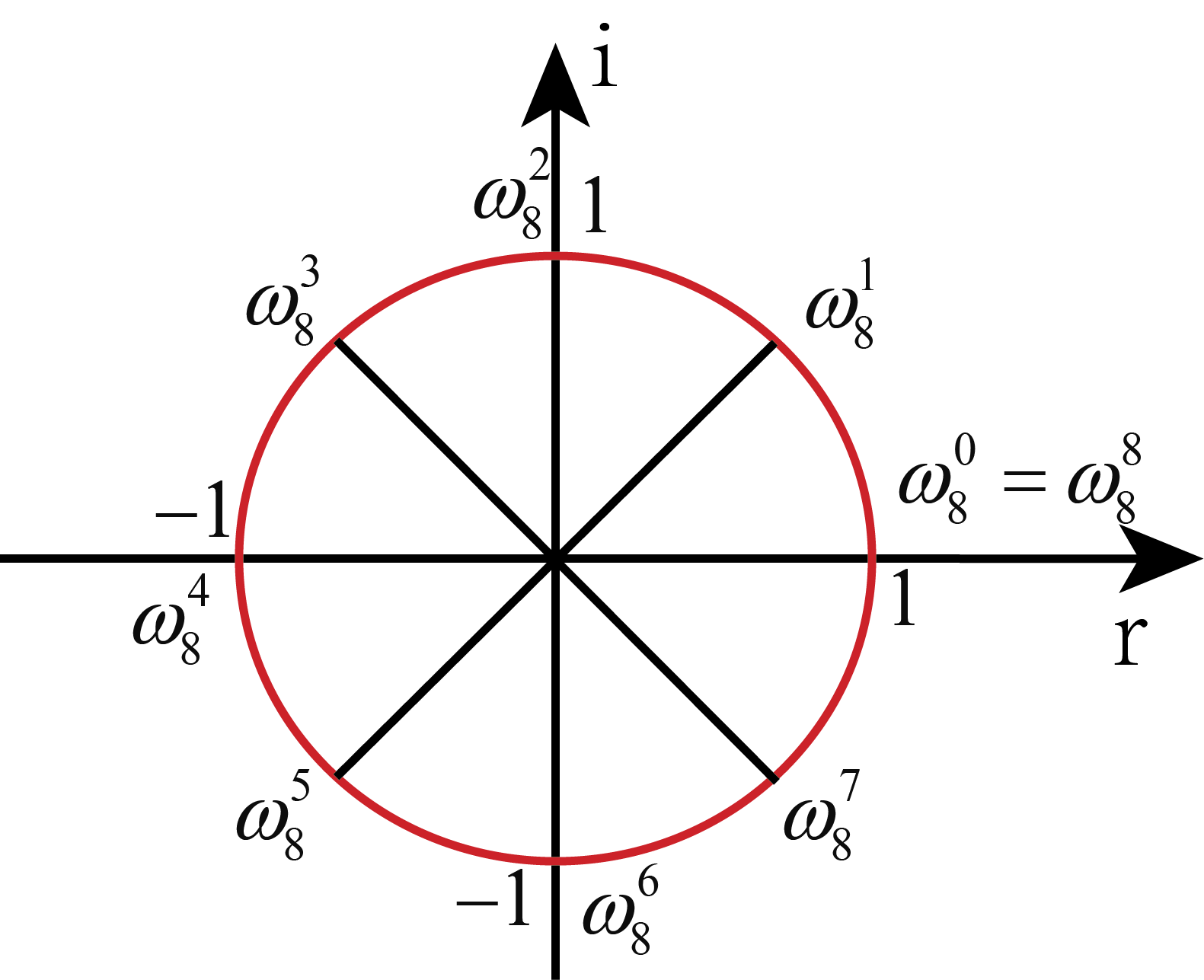
既然点是我们自己选的,那不如使最后一组相反数点对为 ${1,-1}$。我们取 n 等于 8 作为演示。不难看出最后选取的 8 个点均是 $x^8=1$ 的解。
图3 n=8选点示例图
对于任意 $n=2^a , a\in \N$,来说即为 $x^n=1$。
由欧拉公式:
$$
e^{i \theta}=\cos\theta+i\sin\theta
$$
可以得到公式:
$$
z^n=1=\cos2k\pi+i\sin2k\pi=e^{2k\pi i},k \in[ 0,n)
$$
所以:
$$
z=\sqrt[n]{e^{2k\pi i}}=e^\frac{2k\pi i}{n} ,k \in[ 0,n)
$$
上面是 $n$ 次单位复数根的推导。当 $k=1$ 时,值 $\omega_n=e^\frac{2\pi i}{n}$ 被成为主 $n$ 次单位复数根,其他的 $n$ 次单位根都是 $\omega_n$ 的幂次。其中 $\theta$ 表示为复平面单位圆上的弧长。因此 $e^\frac{2\pi i}{n}$ 表示将一个单位圆均分 $n$ 份。$n=8$ 时如下图所示。
图4 8次单位根示意图
$n$ 次单位根的性质:
消去引理:
$$
\omega_{dn}^{dk}=\omega_n^k\\
\omega_{n}^{\frac{n}{2}}=-\omega_2=-1\\
\omega_{n}^{k+\frac{n}{2}}=-\omega_n^k
$$
折半引理:
$$
(\omega_n^k)^2=\omega_{\frac{n}{2}}^k
$$
求和引理:
$$
\sum_{i=0}^{n-1} (\omega_n^k)^i =
\begin{cases}
0, & k \neq mn, \ m \in \mathbb{Z} \\
n, & k = mn, \ m \in \mathbb{Z}
\end{cases}
$$
1.2 $DFT$ 与 $IDFT$
经过 1.1 节的介绍已经对多项式乘法的相关内容有了相应的了解,下面开始正式介绍 $DFT$ 与 $IDFT$,将在 1.3 节介绍 $FFT$ 与 $IFFT$ 的相关内容。我们是从多项式乘法引入的$DFT$和$IDFT$,但是$DFT$和$IDFT$的应用的场景有很多,多项式求值、大数乘法,拉格朗日插值、矩阵乘法、中国剩余定理以及环同态。
1.2.1 离散傅里叶变换($DFT$)
设有一个 $n-1$ 次的多项式 $P(x)$:
$$
P(x) = a_0 + a_1x + a_2x^2 + \ldots + a_{n-1}x^{n-1}
$$
多项式 $P(x)$ 的 $DFT$ 在单位根 $\omega_n^k = e^{2\pi i k / n} $ 上的值计算如下:
$$
P_k = P(\omega_n^k) = \sum_{j=0}^{n-1} a_j \omega_n^{kj} \quad k = 0, 1, \ldots, n-1
$$
1.2.2 逆离散傅里叶变换($IDFT$)
对 $DFT$ 过程我们可以通过矩阵进行描述 $y=Wa$:
$$
\left[ \begin{array}{c}
y_0 \\
y_1 \\
y_2 \\
\vdots \\
y_{n-1} \\
\end{array} \right]
=
\left[ \begin{array}{cccc}
1 & 1 & \ldots & 1 \\
1 & \omega_n & \ldots & \omega_n^{n-1} \\
1 & \omega_n^2 & \ldots & \omega_n^{2(n-1)} \\
\vdots & \vdots & \ddots & \vdots \\
1 & \omega_n^{n-1} & \ldots & \omega_n^{(n-1)^2}
\end{array} \right]
\left[ \begin{array}{c}
a_0 \\
a_1 \\
a_2 \\
\vdots \\
a_{n-1} \\
\end{array} \right]
$$
其中 $V_n$ 是一个范德蒙矩阵,是一个可逆矩阵,因此 $IDFT$:$a=W^{-1}y$。
下面求取:$W_n^{-1}$。矩阵 $W$ 可以表示为:$W_{jk}=ω_ n^{jk}$。$W_{jk}^{-1}$ 的值应该是 $W_{jk}$ 的共轭除以 $n$。由 $\omega _n$ 的性质,我们知道 $\omega _n^k$ 的共轭是 $\omega _n^{-k}$。因此 $W_{jk}^{-1}=\frac{1}{n}ω_ n^{-jk}$。所以 $DFT$ 和 $IDFT$ 的时间复杂一致,甚至计算流程基本一致。
$$
a_j= \frac{1}{n}\sum_{j=0}^{n-1} y_j ω_ n^{-jk} \quad k = 0, 1, \ldots, n-1
$$
1.3 快速傅里叶变化($FFT$)
其实 $FFT$ 的思路在 1.1.3 节中进行了介绍只是并不是很完善,下面进行一个较为细致的描述。详细介绍 FFT 的递归实现和迭代实现。
1.3.1 $FFT$ 递归实现
将单位根带入公式(7)得:
$$
\begin{align}
P(\omega_n^k)=P_e((\omega_n^k)^2)+{\omega_n^k}P_o((\omega_n^k)^2) \quad k \in[ 0,n)
\end{align}
$$
根据消去引理推导出得对称性以及折半引理对公式(8)进行化简。取 $k \in[0,\frac{n}{2})$ 。
$$
\begin{align*}
P(\omega_{n}^{k})&=P_{e}((\omega_{n}^{k})^2)+{\omega_{n}^{k}}P_{o}((\omega_{n}^{k})^2)\\
& =P_{e}(\omega_{\frac{n}{2}}^{k})+{\omega_{n}^{k}}P_{o}(\omega_{\frac{n}{2}}^{k})\\
\end{align*}
$$
$$
\begin{align*}
P(\omega_{n}^{k+m})&=P_{e}((\omega_{n}^{k+m})^2)+\omega_{n}^{k+m}P_{o}((\omega_{n}^{k+m})^2)\\
& =P_{e}(\omega_{\frac{n}{2}}^{k+m})+\omega_{n}^{k+m}P_{o}(\omega_{\frac{n}{2}}^{k+m})\\
& =P_{e}(-\omega_{\frac{n}{2}}^{k})-\omega_{n}^{k}P_{o}(-\omega_{\frac{n}{2}}^{k})\\
& =P_{e}(\omega_{\frac{n}{2}}^{k})-\omega_{n}^{k}P_{o}(\omega_{\frac{n}{2}}^{k})
\end{align*}
$$
即公式(9-10),这两个式子也被称为 CT(Cooley-Tukey)蝶形操作,$\omega_{n}^{k}$ 被成为转换因子。
$$
\begin{align}
P(\omega_{n}^{k})=P_{e}(\omega_{\frac{n}{2}}^{k})+{\omega_{n}^{k}}P_{o}(\omega_{\frac{n}{2}}^{k})\\
P(\omega_{n}^{k+m})=P_{e}(\omega_{\frac{n}{2}}^{k})-\omega_{n}^{k}P_{o}(\omega_{\frac{n}{2}}^{k})
\end{align}
$$
现在给出递归版本得算法:
$$
\begin{array}{ll}
\hline
\text{\textbf{Algorithm 1}} & \text{ Recursion FFT}\\
\hline
\textbf{Require:} & P=[p_0,p_1,\ldots,p_{n-1}]\quad n=2^{a},a\in\mathbb{N}\\
\text{\textbf{function}} & \text{FFT\_R}(P)\\
&n\leftarrow len(P)\\
&\text{if}\quad n==1 \\
&\quad \text{return}\quad P\\
&\text{endif}\\
&\omega_n \leftarrow e^{\frac{2\pi i}{n}}\\
&P_e\leftarrow [p_0,p_2,\ldots,p_{n-2}]\\
&P_o\leftarrow [p_1,p_3,\ldots,p_{n-1}]\\
&y_e\leftarrow FFT\_R(P_e)\\
&y_o\leftarrow FFT\_R(P_o)\\
& \text{for} \quad k \quad \text{to} \quad \frac{n}{2}-1\\
&\quad y[k]=y_e[k]+\omega_n^ky_o[k]\\
&\quad y[k+\frac{n}{2}]=y_e[k]-\omega_n^ky_o[k]\\
&\text{endfor}\\
&\text{return} \quad y \\
\textbf{end function} & \\
\hline &
\end{array}
$$
蝶形操作:
蝶形操作得名于其数据流图的形状,上面的推导过程出现的是 CT 蝶形变换,还有一种 GS 蝶形变换。
图5 CT蝶形操作图
图6 CT蝶形操作简化图
通过公式(9-10)我们可以推导出 GS 蝶形变换的形式。将公式(9)和(10)分别加减运算得:
$$
P(\omega_{n}^{k}) + P(\omega_{n}^{k+m}) = 2P_{e}(\omega_{\frac{n}{2}}^{k})
\\
P(\omega_{n}^{k}) - P(\omega_{n}^{k+m}) = 2\omega_{n}^{k}P_{o}(\omega_{\frac{n}{2}}^{k})
$$
整理得公式(11-12)不难看出,GS 操作是 CT 操作的逆过程,可以用于 $IFFT$ 中,当然也可以用在$FFT$中,通常CT方法也叫$DIT$(时域抽取)操作,GS操作也叫$DIF$(频域抽取)操作。
$$
\begin{align}
P_e(\omega_{\frac{n}{2}}^{k}) &= \frac{1}{2}(P(\omega_{n}^{k}) + P(\omega_{n}^{k+m})) \\
P_o(\omega_{\frac{n}{2}}^{k}) &= \frac{1}{2\omega_{n}^{k}}(P(\omega_{n}^{k}) - P(\omega_{n}^{k+m}))
\end{align}
$$
图7 GS蝶形操作
1.3.2 $FFT$ 迭代实现
继续优化。依然拿 n=8 举例。递归数据操作如图 7 所示,在递归操作中是自定向下层层展开,然后逐层向上收缩。每一次递归都会消耗堆栈资源,影响效率。如果可以从底向上计算,那么可以省去堆栈资源的消耗,提高程序运行效率。于是现在的问题就变为了如何确定递归树叶子节点的元素排序。
图8 n=8时递归示意图
位逆序 将叶子节点元素顺序和原始元素顺序均使用二进制表示。发现二进制表示发生了左右对称反转,称之为位逆序变换。
1
2
3
4
5
//位逆序
Layer 4 : 0 4 2 6 1 5 3 7
Binary : 000 100 010 110 001 101 011 111
Reverse : 000 001 010 011 100 101 110 111
Decimal : 0 1 2 3 4 5 6 7
下面是 Bit-Reverse-Copy 的实现:
$$
\begin{array}{ll}\hline\text{\textbf{Algorithm 2}} & \text{Bit-Reverse-Copy}\\ \hline\text{\textbf{Require:}} & A\\ \text{\textbf{function}} & \text{BitReverseCopy}(A)\\ & n\leftarrow len(A)\\ & b\leftarrow\log_2(n)\\ & \text{for}\quad i=0\quad\text{to}\quad n-1\\ & \quad r\leftarrow\text{ReverseBits}(i,b)\\ & \quad B[r]\leftarrow A[i]\\ & \text{endfor}\\ & \text{return}\quad B\\ \text{\textbf{end function}} & \phantom{}\\ \hline & \phantom{}\end{array}
$$
函数 ReverseBits 的实现如下,基本过程就是取原值低位赋值给目标值低位,然后原值右移一位,目标值左移一位,直到循环结束。
$$
\begin{array}{ll}
\hline
\text{\textbf{Function}} & \text{ReverseBits}(i, b) \\
\hline
& result \leftarrow 0 \\
& \text{for}\quad j = 0\quad\text{to}\quad b - 1 \\
& \quad result \leftarrow result \ll 1 \\
& \quad bit \leftarrow (i \gg j) \& 1 \\
& \quad result \leftarrow result \, | \, bit \\
& \text{endfor} \\
& \text{return}\quad result \\
\hline
\end{array}
$$
迭代算法实现
算法 3 是$DIT$实现,算法4是$DIF$实现。$s $ 可以看作是合并轮数。$m$ 是当前合并次数下每个单元的规模。其中$\hat{1}$是乘法单位元都是$\omega_n^0$。这里的$\omega_n=e^{\pm2\pi i / n}$,在进行$FFT$操作时取正,$IFFT$操作时取负。当然IFFT还需要乘上$n^{-1}$。
$$
\begin{array}{ll}\hline\text{\textbf{Algorithm 3}} & \text{DIT}\\
\hline
\text{\textbf{Require:}} & A=[a_0,a_1,\ldots,a_{n-1}]\quad n=2^{x},x\in\mathbb{N}\\ \text{\textbf{function}} & \text{DIT}(A)\\
& n\leftarrow len(A)\\
& P\leftarrow BitReverseCopy(A)\\
& \text{for}\quad s=1\quad\text{to}\quad \log_2n\\
& \quad m=2^s\\
& \quad \omega_m=\omega_n^{\frac{n}{m}}\\
& \quad\text{for}\quad k=0\quad \text{to} \quad n-1 \quad \text{by}\quad m\\
& \quad\quad \varphi=\hat{1}\\
& \quad\quad\text{for}\quad j=0\quad\text{to} \quad \frac{m}{2}-1\\
& \quad\quad\quad t=\varphi P[k+j+\frac{m}{2}]\\
& \quad\quad\quad u= P[k+j]\\
& \quad\quad\quad P[k+j]= u+t\\
& \quad\quad\quad P[k+j+\frac{m}{2}]= u-t\\
& \quad\quad\quad \varphi=\varphi \omega_m\\
& \quad\quad\text{endfor}\\
& \quad\text{endfor}\\
& \text{endfor}\\
& \text{return}\quad P\\
\text{\textbf{end function}}
& \\
\hline
& \end{array}
$$
$$
\begin{array}{ll}\hline\text{\textbf{Algorithm 4}} & \text{DIF}\\
\hline
\text{\textbf{Require:}} & A=[a_0,a_1,\ldots,a_{n-1}]\quad n=2^{x},x\in\mathbb{N}\\ \text{\textbf{function}} & \text{DIF}(P)\\
& n\leftarrow len(A)\\
& P\leftarrow A\\
& \text{for}\quad s=\log_2n \quad\text{to}\quad 1\\
& \quad m=2^s\\
& \quad \omega_m=\omega_n^{\frac{n}{m}}\\
& \quad\text{for}\quad k=0\quad \text{to} \quad n-1 \quad \text{by}\quad m\\
& \quad\quad \varphi=\hat{1}\\
& \quad\quad\text{for}\quad j=0\quad\text{to} \quad \frac{m}{2}-1\\
& \quad\quad\quad t= P[k+j+\frac{m}{2}]\\
& \quad\quad\quad u= P[k+j]\\
& \quad\quad\quad P[k+j]= u+t\\
& \quad\quad\quad P[k+j+\frac{m}{2}]= \varphi(u-t)\\
& \quad\quad\quad \varphi=\varphi \omega_m\\
& \quad\quad\text{endfor}\\
& \quad\text{endfor}\\
& \text{endfor}\\
& P\leftarrow BitReverseCopy(P)\\
& \text{return}\quad P\\
\text{\textbf{end function}}
& \\
\hline
& \end{array}
$$
下面是 n=8 时,$DIT$迭代 $FFT$ 的数据流图。
图9 n=8迭代DIT数据流图
1.4 快速数论变换($NTT$)
$FFT$ 存一些问题。首先 FFT 是在复数域上的表示,而计算机系统中表示复数,需要比实数花费更多的资源,且复数运算也比实数运算更加复杂。此外 FFT 涉及大量的正余弦运算,对于精度有影响。于是我们期望在实数域内寻找类似单位根性质的数学概念。有限域上的原根满足相应的要求。
1.4.1 数学基础
欧拉函数
欧拉函数,即 $\varphi(n)$,表示的是小于等于 $n$ 且和 $n$ 互素的数的个数。当 n 是素数时 $\varphi(n)=n-1$。
欧拉定理
对于 $a \in \Z$ ,$m\in \N^*$,若 $\gcd(a,m)=1$,则 $a^{\varphi(m)} \equiv 1 \pmod{m}$。
费马小定理
若 $p $ 为素数,$\gcd(a,p)=1$,则 $a^{p-1} \equiv 1 \pmod{p}$。
也可表达为,对于任意整数 $a $,有 $a^p \equiv a \pmod{p}$。
利用费马小定理求逆元:$a^{-1}=a^{p-2}$
阶
由欧拉定理可知,若 $\gcd(a,p)=1$,一定存在一个最小的正整数 $n$ 满足同余式 $a^n \equiv 1 \pmod{m}$。这个 $n$ 被称作 $a$ 模 $m$ 的阶记作 $\delta_m(a) $ 或者 $ord_m(a)$。具有以下性质:
性质 1:$a,a^2,\ldots,a^{\delta_m(a)}$ 模 $m $ 两两不同余,之后进入周期。
性质 2:若 $a^n \equiv 1 \pmod{m}$,则 $\delta_m(a)|n$。可以推导出若 $a^p \equiv a^q \pmod{m} $,则有 $p \equiv q \pmod{\delta_m(a)}$。
原根
给定 $n \in \N^*$ ,$g \in \Z$,满足 $\gcd(g, m) = 1$,且 $\delta_m(g) = \varphi(m)$ ,则称 $g$ 为模 $m$ 的原根。
即 $g$ 满足 $\delta_m(g)=| \Z_m^* |=\varphi(m)$ 。当 $m$ 是素数时,我们有 $g^i \mod m$,$0<i<m$ 的结果互不相同
原根个数:若一个数 $m$ 有原根,则它原根的个数为 $\varphi(\varphi(m))$。
原根存在定理:一个数 $m$ 存在原根当且仅当 $m=2,4,p^a,2p^a$ ,其中 $p$ 为奇素数,$a\in \N^*$。
原根的性质
原根具有以下性质,不难看与单位根具有类似的性质。所以可以用于替代单位根,用于简化 $DFT$ 计算。
不重性:$\forall 0 \leq i < j < \varphi(p),\ g^i \not\equiv g^j \pmod{p} $
折半性:定义 $g_n = g^{\frac{1}{n}} \equiv g^{\frac{p-1}{n}}$,$g_n^k = (g_n)^k$ 则 $g_{an}^{ak} \equiv g_n^k \pmod{p}$。
对称性:$g_{2n}^{k+n} \equiv - g_{2n}^k \pmod{p}$
求和性:$\sum_{i=0}^{n-1} (g_n)^{ki} \equiv n[k=0] \pmod{p} $,$k=0$ 为真 $[k=0]=1$,否则为 $0$。
原根与模数的选择
为了实现多次二分,模数 $p$ 应选可以拆分为 $q\times 2^k +1$ 的素数,$q$ 为奇素数,$k$ 为整数,$2^k$ 模数的阶,也就是原根的最大数量。可以看下表的例子。
$$
\text{表 1:原根和模数的相关数据}\\
\begin{array}{cccc}
\hline
\text{原根 } g & \text{模数 } p & \text{分解 } p & \text{模数的阶} \\
\hline
3 & 469762049 & 7 \times 2^{26} + 1 & 2^{26} \\
3 & 998244353 & 119 \times 2^{23} + 1 & 2^{23} \\
3 & 2281701377 & 17 \times 2^{27} + 1 & 2^{27} \\
\hline
\end{array}
$$
1.4.2 $NTT$ 的递归实现
将原根带入公式(7)得:
$$
\begin{align}
P(g_n^k)=P_e((g_n^k)^2)+{g_n^k}P_o((g_n^k)^2)\mod p \quad k \in[ 0,n)
\end{align}
$$
根据消去引理推导出得对称性以及折半引理对公式(13)进行化简。取 $k \in[0,\frac{n}{2})$ 。
$$
\begin{align*}
P(g_{n}^{k})&=P_{e}((g_{n}^{k})^2)+{g_{n}^{k}}P_{o}((g_{n}^{k})^2) \mod p\\
& =P_{e}(g_{\frac{n}{2}}^{k})+{g_{n}^{k}}P_{o}(g_{\frac{n}{2}}^{k}) \mod p\\
\end{align*}
$$
$$
\begin{align*}
P(g_{n}^{k+m})&=P_{e}((g_{n}^{k+m})^2)+g_{n}^{k+m}P_{o}((g_{n}^{k+m})^2) \mod p\\
& =P_{e}(g_{\frac{n}{2}}^{k+m})+g_{n}^{k+m}P_{o}(g_{\frac{n}{2}}^{k+m}) \mod p\\
& =P_{e}(-g_{\frac{n}{2}}^{k})-g_{n}^{k}P_{o}(-g_{\frac{n}{2}}^{k}) \mod p\\
& =P_{e}(g_{\frac{n}{2}}^{k})-g_{n}^{k}P_{o}(g_{\frac{n}{2}}^{k}) \mod p
\end{align*}
$$
简化为:
$$
P(g_{n}^{k})=P_{e}(g_{\frac{n}{2}}^{k})+{g_{n}^{k}}P_{o}(g_{\frac{n}{2}}^{k})\\
P(g_{n}^{k+m})=P_{e}(g_{\frac{n}{2}}^{k})-g_{n}^{k}P_{o}(g_{\frac{n}{2}}^{k})
$$
现在给出递归版本得算法,不难发现除了将单位根替换为原根,增加模运算,以及增加了参数 ,原根 $g$,模数 $p $ 外与 $FFT$ 并无太大区别。
$$
\begin{array}{ll}
\hline
\text{\textbf{Algorithm 5}} & \text{ Recursion Number Theoretic Transform (NTT)}\\
\hline
\textbf{Require:} & A=[a_0,a_1,\ldots,a_{n-1}],\quad n=2^{k},\quad g ,\quad p \\
\text{\textbf{function}} & \text{NTT\_R}(A, g, p)\\
&n\leftarrow \text{len}(A)\\
&\text{if}\quad n==1 \\
&\quad \text{return}\quad A\\
&\text{endif}\\
&g_n \leftarrow g^{\frac{p-1}{n}} \pmod p\\
&A_e\leftarrow [a_0,a_2,\ldots,a_{n-2}]\\
&A_o\leftarrow [a_1,a_3,\ldots,a_{n-1}]\\
&Y_e\leftarrow \text{NTT\_R}(A_e, g_n^2, p)\\
&Y_o\leftarrow \text{NTT\_R}(A_o, g_n^2, p)\\
& \text{for} \quad k \quad \text{from} \quad 0 \quad \text{to} \quad n/2-1\\
&\quad Y[k]= (Y_e[k] + g_n^k Y_o[k]) \pmod p\\
&\quad Y[k+n/2]= (Y_e[k] - g_n^k Y_o[k]) \pmod p\\
&\text{end for}\\
&\text{return} \quad Y \\
\textbf{end function} & \\
\hline &
\end{array}
$$
注意NTT里的$g^{-1}$是取逆元操作,在计算$INTT$时请注意。
1.4.3 $NTT$ 的迭代实现
$NTT$ 的迭代实现同理,因此不再赘述,直接给出相应的算法。
$$
\begin{array}{ll}
\hline
\text{\textbf{Algorithm 6}} & \text{Iteration NTT}\\
\hline
\text{\textbf{Require:}} & A=[a_0,a_1,\ldots,a_{n-1}],\ n=2^{k},\quad g, \quad p\\
\text{\textbf{function}} & \text{NTT\_I}(A, g, p)\\
& n \leftarrow \text{len}(A)\\
& P \leftarrow \text{BitReverseCopy}(A)\\
& \text{for}\ s=1\ \text{to}\ \log{n}\\
& \quad m=2^s\\
& \quad g_m=g^{\frac{n}{m}} \pmod p\\
& \quad \text{for}\ k=0\ \text{to}\ n-1\ \text{by}\ m\\
& \quad\quad \varphi=\hat{1}\\
& \quad\quad \text{for}\ j=0\ \text{to}\ \frac{m}{2}-1\\
& \quad\quad\quad t=\varphi P[k+j+\frac{m}{2}] \pmod p\\
& \quad\quad\quad u= P[k+j] \pmod p\\
& \quad\quad\quad P[k+j]= (u+t) \pmod p\\
& \quad\quad\quad P[k+j+\frac{m}{2}]= (u-t) \pmod p\\
& \quad\quad\quad \varphi=(\varphi \cdot g_m) \pmod p\\
& \quad\quad \text{endfor}\\
& \quad \text{endfor}\\
& \text{endfor}\\
& \text{return}\ P\\
\text{\textbf{end function}} & \\
\hline
&
\end{array}
$$
1.5 矩阵DFT算法
现在介绍另外一种算法,这种算法提高缓存命中率,从而提高执行效率。这种算法是将输入看作是一个行优先的矩阵进行计算,请注意对于NTT来说实际的输入指的是系数$a_i$。
如果 $n=R\cdot C$ 我们可以用 $i_r\in[0,R)$ 和 $i_c \in [0,C)$ 重写$i=i_r\cdot C+i_c$ 。这将创建一个对应 $[0,n) \backsimeq[0,R) \times[0,C)$。另一种对应关系是 $k=k_r+k_c\cdot R$ ,注意这里输出的顺序已经变成了列优先了。将$i$和$k$带入下式。
$$
P_{k}=P(\omega_{n}^{k})=\sum_{i=0}^{n-1}a_{i}\omega_{n}^{ki}\quad k=0,1,\ldots,n-1
$$
需要提前明确的一点是这里公式中$\omega$既可以是原根又可以是单位根,不过为了统一表示省去了原根的取模操作。替换可得:
$$
\begin{align}P_{k_{r}+k_{c}\cdot R}=\sum_{i_{c}=0}^{C-1}\sum_{i_{r}=0}^{R-1}a_{i_{r}\cdot C+i_{c}}\cdot\omega_{R\cdot C}^{(k_{r}+k_{c}\cdot R)(i_{r}\cdot C+i_{c})}\end{align}
$$
将$\omega$的幂次展开:
$$
\begin{align*}
\omega_{R\cdot C}^{(k_{r}+k_{c}\cdot R)(i_{r}\cdot C+i_{c})}&=\omega_{R\cdot C}^{i_{c}k_{r}+i_{c}k_{c}\cdot R+i_{r}k_{r}\cdot C+i_{r}k_{c}\cdot RC} \\&=\omega_{R\cdot C}^{i_{c}k_{r}}\cdot \omega_{R\cdot C}^{i_{c}k_{c}\cdot R}\cdot \omega_{R\cdot C}^{i_{r}k_{r}\cdot C}\cdot \omega_{R\cdot C}^{i_{r}k_{c}\cdot RC}
\end{align*}
$$
根据原根的折半性质或者单位根的消去引理$\omega_{an}^{ak}=\omega_n^k$,可得:
$$
\omega_{R\cdot C}^{i_{c}k_{r}}\cdot \omega_{R\cdot C}^{i_{c}k_{c}\cdot R}\cdot \omega_{R\cdot C}^{i_{r}k_{r}\cdot C}\cdot \omega_{R\cdot C}^{i_{r}k_{c}\cdot RC}=\omega_{n}^{i_{c}k_{r}}\cdot \omega_{C}^{i_{c}k_{c}}\cdot \omega_{R}^{i_{r}k_{r}}\cdot1
$$
则公式(14)变为如下形式:
$$
P_{k_{r}+k_{c}\cdot R}=\sum_{i_{c}=0}^{C-1}\sum_{i_{r}=0}^{R-1}a_{i_{r}\cdot C+i_{c}}\cdot \omega_{n}^{i_{c}k_{r}}\cdot \omega_{C}^{i_{c}k_{c}}\cdot \omega_{R}^{i_{r}k_{r}}
$$
添加一些括号来确定运算顺序则变成了:
$$
P_{k_{r}+k_{c}\cdot R}=\sum_{i_{c}=0}^{C-1}\Bigg[\bigg(\sum_{i_{r}=0}^{R-1}a_{i_{r}\cdot C+i_{c}}\cdot \omega_{R}^{i_{r}k_{r}}\bigg)\omega_{n}^{i_{c}k_{r}} \Bigg] \omega_{C}^{i_{c}k_{c}}
$$
首先对输入a子序列进行长度为$R$的$DFT$操作,然后对结果乘上旋转因子,最后进行长度为$C$的$DFT$操作。这么看可能不直观,我们将输入写成一个$R \times C$大小的矩阵:
$$
a
=
\left[ \begin{array}{ccccc}
a_0 & a_1 & a_2 &\ldots & a_{C-1} \\
a_C & a_{C+1} & a_{C+2} & \ldots & a_{C+(C-1)} \\
a_{2C} & a_{2C+1} & a_{2C+2} & \ldots & a_{2C+(C-1)} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
a_{(R-1)C} & a_{(R-1)C+1} & a_{(R-1)C+2}& \ldots & a_{(R-1)C+(C-1)}
\end{array} \right]
$$
先对对所有列进行DFT运算,然后所有元素乘上相应的转换因子,最后对所有行进行DFT运算。下面是转换转换因子矩阵$T$,注意转换因子矩阵与对列进行DFT的结果进行的是逐点相乘。因为输出是列优先排序,所以需要对结果进行一个转置,从而使得输入与输出保持同一顺序。
$$
T=\left[\begin{array}{ccccc}
1 & 1 & 1 & \ldots & 1\\
1 & \omega &\omega^2 & \ldots & \omega^{C-1}\\
1 & \omega ^2 & \omega ^4 &\ldots & \omega^{2(C-1)}\\
\vdots & \vdots& \vdots & \ddots & \vdots\\
1 & \omega^{R-1}&\omega^{2(R-1)} & \ldots & \omega^{(C-1)(R-1)}
\end{array}\right]
$$
Four-step DFT
对上面的算法进行一个总结就是所谓的四步DFT算法,$[R \times C]$,表示为大小为$R\times C$的行优先矩阵。
$IDFT*$是省略乘上$n^{-1}$的$IDFT$,所以最后需要补上$n^{-1}$。
DFT:
$[R \times C]$,对每一列进行长度为$R$的$DFT$运算。
$[R \times C]$,所有元素乘上对应的转换因子$\omega^{ik}$。
$[R \times C]$,对每一行进行长度为$C$的$DFT$运算。
$[R \times C]$,将矩阵进行转置。
IDFT*:
$[C \times R]$,将矩阵进行转置。
$[R \times C]$,对每一行进行长度为$C$的$IDFT*$运算。
$[R \times C]$,所有元素乘上对应的转换因子$\omega^{-ik}$。
$[R \times C]$,对每一列进行长度为$R$的$IDFT*$运算。
Six-step DFT
对列进行操作,无法读取连续的内存会影响计算效率,可以增加转置操作,于是获得六步DFT算法:
DFT:
$[R \times C]$,将矩阵进行转置。
$[C \times R]$,对每一行进行长度为$R$的$DFT$运算。
$[C \times R]$,将矩阵进行转置。
$[R \times C]$,所有元素乘上对应的转换因子$\omega^{ik}$。
$[R \times C]$,对每一行进行长度为$C$的$DFT$运算。
$[R \times C]$,将矩阵进行转置。
IDFT*:
$[C \times R]$,将矩阵进行转置。
$[R \times C]$,对每一行进行长度为$C$的$IDFT*$运算。
$[R \times C]$,所有元素乘上对应的转换因子$\omega^{-ik}$。
$[R \times C]$,将矩阵进行转置。
$[C \times R]$,对每一行进行长度为$R$的$IDFT*$运算。
$[C \times R]$,将矩阵进行转置。
2 NTT 设计
本节主要是介绍对NTT的设计,例如模约简方案、转置优化以及预计算。最后探讨有哪些可以进行的优化。
2.1 模约简
2.1.1 朴素方案
在模数约简的朴素方法中,如果硬件支持的话,会使用一个硬件指令将两个字(word)长度的被除数除以一个字长度的除数,得到一个字长度的商和一个字长度的余数。如果硬件不支持这种指令,那么就需要在软件中模拟这种指令。
这样的指令在x86和x86-64架构中是存在的。对于软件模拟,GNU GCC和Clang编译器在32位平台上提供了uint64_t类型,在64位平台上提供了unsigned __int128类型,并且这些类型都支持除法操作。
2.1.2 Barrett 约简
巴雷特约简的思路很简单,将计算$z =a \mod p$,转换为$z=a- tp,t=\lfloor ap^{-1}\rfloor$ 。于是问题就从模运算转换为了求取$p^{-1}$的近似值,也就是$t$的近似值。
对$t$进行进行变换:
$$
t=\lfloor \frac{a}{p} \rfloor=\lfloor \frac{\frac{a}{b^{k-1}}\frac{b^{2k}}{p}}{b^{k+1}} \rfloor
$$
其中$b$是基底,计算机系统中通常使用二进制表示,即$b=2$,$k$是模数相对于基底的位宽$k=\log_{b}p+1$,之所以是$b^{2k}$是因为通常运用模约简的场景是模乘,因此$a\in[0,p^2)$。经过变换,我们发现分离出来一个一个仅和模数有关的量:$\alpha = \frac{b^{2k}}{p}$,这意味着对同一模数的约简可以提前计算$\alpha$,其他部分可以通过右移和乘法完成,乘法运算效率显著高于除法运算,位移效率更快,计算速度提升了很多。
为了避免浮点数计算,令$\beta=\lfloor \frac{b^{2k}}{p} \rfloor$,替换掉$\alpha$,得到$t$的近似$\hat{t}$:
$$
\hat{t}=\lfloor \frac{\lfloor\frac{a}{b^{k-1}}\rfloor \beta}{b^{k+1}} \rfloor=\lfloor \frac{\lfloor\frac{a}{b^{k-1}}\rfloor \lfloor \frac{b^{2k}}{p} \rfloor}{b^{k+1}} \rfloor
$$
现在考虑$t$与$\hat{t}$的误差:
$$
\lambda = \frac{a}{b^{k-1}} - \lfloor \frac{a}{b^{k-1}} \rfloor
$$
$$
\mu = \frac{b^{2k}}{p} - \lfloor \frac{b^{2k}}{p} \rfloor
$$
且$0 \le \lambda \lt 1$,$0 \le \mu \lt 1$,此外还有:
$$
t=\lfloor\frac{a}{b^{k-1}}\cdot\frac{b^{2k}}{p}\cdot\frac{1}{b^{k+1}}\rfloor=\lfloor\frac{(\lfloor\frac{a}{b^{k-1}}\rfloor+\lambda)(\lfloor\frac{b^{2k}}{p}\rfloor+\mu)}{b^{k+1}}\rfloor\leq\lfloor\hat{t}+\frac{\lfloor\frac{a}{b^{k-1}}\rfloor+\lfloor\frac{b^{2k}}{p}\rfloor+1}{b^{k+1}}\rfloor
$$
因为$a\lt b^{2k}$,所以$\lfloor \frac{a}{b^{k-1}} \rfloor \leq b^{k+1}-1$;又因为$p \ge b^{k-1}$,所以$\lfloor \frac{b^{2k}}{p}\rfloor \leq b^{k+1}$。对上面不等式放缩:
$$
t\leq\lfloor\hat{t}+\frac{b^{k+1}-1+b^{k+1}+1}{b^{k+1}}\rfloor=\lfloor\hat{t}+2\rfloor
$$
又因为$\hat{t} \le t$,所以可得:
$$
t-2 \le \hat{t} \le t
$$
近似性不错,进一步可得:
$$
0 \lt a - \hat{t}p \le a - (t-2)p=a-tp+2p
$$
又因为$a-tp=z\lt p$,所以:
$$
0 \lt a - \hat{t}p \lt 3p
$$
不难看出使用近似方法得出得值有可能比p大,但是通过最多两次减法就可以修正误差,下面给出完整的算法:
$$
\begin{array}{ll}
\hline
\text{\textbf{Algorithm 7}} & \text{Barrett 约简}\\
\hline
\text{\textbf{Require:}} & a\quad \beta=\lfloor \frac{b^{2k}}{p} \rfloor\quad p\\
\text{\textbf{function}} & Barrett(a,\beta,p)\\
& \hat{t} \leftarrow \lfloor \frac{\lfloor\frac{a}{b^{k-1}}\rfloor \beta}{b^{k+1}} \rfloor\\
& z_1 \leftarrow a \mod b^{k+1}\\
& z_2 \leftarrow \hat{t}\cdot p \mod b^{k+1}\\
& z=z_1-z_2\\
& \text{if} \ z \lt 0\\
& \quad z=z+b^{k+1}\\
& \text{endif}\\
& \text{while} \ z \ge p\\
& \quad z=z-p\\
& \text{endwhile}\\
& \text{return}\ z\\
\text{\textbf{end function}} & \\
\hline
&
\end{array}
$$
$z_1$和$z_2$的运算可以通过位与操作直接去掉k位的高位即可,简化了计算。下面给出$\beta$的算法:
$$
\begin{array}{ll}
\hline
\text{\textbf{Algorithm 8}} & \text{计算} \beta\\
\hline
\text{\textbf{Require:}} & p\quad k \quad b\\
\text{\textbf{function}} & get\beta(p,k,b)\\
& \beta \leftarrow b^k\\
& \text{repeat} \\
& \quad s \leftarrow \beta \\
& \quad \beta \leftarrow 2\beta -\lfloor\frac{ p\lfloor \frac{\beta^2}{b^k} \rfloor }{b^k} \rfloor\\
& \text{until} \ \beta \le s \\
& t \leftarrow b^{2k}-p\beta\\
& \text{while} \ t \lt 0\\
& \quad \beta \leftarrow \beta -1\\
& \quad t \leftarrow t+p\\
& \text{endwhile}\\
& \text{return}\ \beta\\
\text{\textbf{end function}} \\
\hline
&\end{array}
$$
2.1.3 Montgomery 约简
蒙哥马利模乘约减的思路是通过变换,将需要取模的数控制到很小的范围($[0,(p-1)^2] \rightarrow [0,2p-1]$ )然后通过少量减法获取最后结果。并通过位运算简化计算,例如:右移除法、位与取模。
蒙哥马利约简
对于$\forall t \in \Z$且满足$a < r p$,$r\gt p$,$\gcd(r,p)=1$ 。$p$是以$b$为基底,长度为$k$的整数,则r的取值为$b^k$,计算机中$b$为$2$,显然$r\gt p$。但是只有当$\gcd(b,p)=1$时才满足$\gcd(r,p)=1$,之前提到的格式是满足条件的。
由于$r$和$p$互素,所以存在$r’,p’ \in[0,p)$使得下式成立,$r’$是$r$在$p$下的逆元 ,$p’$是$p$在$r$下的负逆元。
$$
rr'-pp'=1
$$
于是:
$$
\begin{align*}
ar' &=ar'\frac{r}{r} \\
&=\frac{arr'}{r} \\
&=\frac{a(1+pp')}{r} \\
&=\frac{a+app'}{r} \\
&=\frac{a+(\lfloor \frac{ap'}{r} \rfloor r+(ap' \bmod r))p}{r} \\
&=\frac{a+(ap' \bmod r)p}{r}+\lfloor \frac{ap'}{r} \rfloor p \\
&\equiv \frac{a+(ap' \bmod r)p}{r} &\pmod{p} \\
&\equiv \frac{a+((a\bmod r)p' \mod r)p}{r} &\pmod{p} \\
\end{align*}
$$
其中$\lfloor \frac{ap’}{r} \rfloor r+(ap’ \bmod r)$是将$ap’$表达为成商乘上除数加余数的形式。上面的推导过程将对$ar’$模$p$转换为了对$\frac{a+((a\bmod r)p’ \bmod r)p}{r}$模$p$操作。显然$((a\mod r)p’ \mod r)p \lt rp$又因为$a < r p$所以可得下面的关系,不难发现最多只需一次减法就可以完成取模操作,其中模$r$可以通过位与运算,除$r$可以通过位右移运算完成,之所以做两次模$r$运算是为了降低乘法位宽。
$$
\frac{t+((t\mod r)p' \mod r)p}{r} \lt 2p
$$
下面给出相应的算法:
$$
\begin{array}{ll}
\hline
\text{\textbf{Algorithm 8}} & \text{蒙哥马利约简} \\
\hline
\text{\textbf{Require:}} & p\quad r \quad p' \quad (pp' \equiv-1\mod r )\quad \\
\text{\textbf{function}} & REDC(a)\\
& \beta \leftarrow b^k\\
& m \leftarrow (a\bmod r)p' \bmod r \\
& t \leftarrow (a+mp) \text{div }r \\
& \text{if} \ t \gt p\\
& \quad \quad \text{return}\ t-p\\
& \text{else} \\
& \quad \quad \text{return}\ t\\
& \text{endif}\\
\text{\textbf{end function}} \\
\hline
&\end{array}
$$
蒙哥马利域
由上面蒙哥马利约简的过程不难发现实际是对$xR^{-1}$(这里的$R^{-1}$就是上面提到的$r’$,只是为了方便区分)进行约简,所以在使用蒙哥马利约简时,首先需要转换到蒙哥马利域中,蒙哥马利域中的形式表示为$\bar{x}$,转换入蒙哥马利域的方式:
$$
\bar{x} =x \cdot R \pmod p
$$
显然,转入蒙哥马利域的成本是高昂的,只有在蒙哥马利域内计算值得时才会使用蒙哥马利约简,在蒙哥马利域中加法和减法(结合律)不受影响。
$$
\bar{x}+\bar{y} = xR+yR=(x+y)R = \overline{x+y} \pmod p
$$
但是蒙哥马利域上的乘法是不正确的,这里蒙哥马利域中的乘法用 $\times$表示,正常的乘法用$\cdot$表示。我们期望的结果是:
$$
\bar{x}\times\bar{y}=\overline{x\cdot y}=(x\cdot y) R \pmod{p}
$$
但是实际上如果直接相乘获得结果如下:
$$
\bar{x}\cdot\bar{y}=xR\cdot yR=(x\cdot y) RR \pmod{p}
$$
蒙哥马利域上的乘法定义如下:
$$
\bar{x}\times\bar{y}=(\bar{x}\cdot \bar{y}) R^{-1} =(x\cdot y) R=RECD(\bar{x}\cdot \bar{y})\pmod{p}
$$
最后就是蒙哥马利域的转出,转出如下所示。
$$
x = \bar{x}\cdot R^{-1}=RECD(\bar{x}) \pmod p
$$
蒙哥马利模乘
在执行蒙哥马利乘法本身开销并不高,但是需要完成一些提前计算,这些计算的开销较高。
蒙哥马利域的转入
$p’$的计算
蒙哥马利域的转出
在约简过程中已经完成了蒙哥马利域的转出。p’的计算可以通过扩展欧几里得算法获得。对于转入还存在另一种策略:
$$
\bar{x} =x \cdot R \mod{p} =x \times R^2 =REDC(x\cdot (R^2 \mod p))
$$
第二种策略策略是省去模p的运算,但是失去了乘R位运算优势,取而代之的是乘上$R^2 \mod p$,可以提前计算,并需要执行约简操作,因为取模开销很大,大概率第二种策略效率更高一点。于是蒙哥马利模乘可以表示如下:
$$
\begin{align*}
z&=x\cdot y \mod p=REDC(REDC(\bar{x}\cdot \bar{y}))\\
\bar{x}&=REDC(x\cdot (RR \bmod p))\\
\bar{y}&=REDC(y\cdot (RR \bmod p))\\
\end{align*}
$$
2.1.4 小结
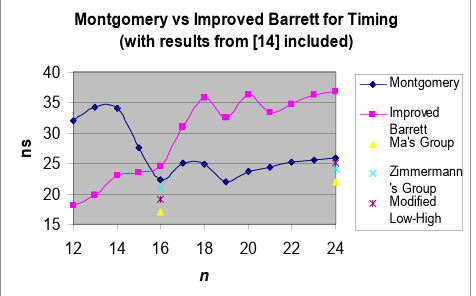
上面介绍了三种模约简方法,模约简主要用于模乘中,这里主要对比分析一下巴雷特和蒙哥马利,至于朴素方案效率太低就不分析了。在FPGA上当一次处理位宽大于$16$-bit时蒙哥马利更具有优势,反之巴列特算法有优势IEEE Comparison of Montgomery and Barrett modular multipliers on FPGAs 。对CPU或者GPU版本没有看到相应的资料,不过从两种算法从时间复杂度上是类似的Efficient Randomized Regular Modular Exponentiation using Combined Montgomery and Barrett Multiplications 。连续模乘可能蒙哥马利的优势更大。
图 10 FPGA蒙哥马利与巴雷特对比
2.2 root power 预计算
算法3中需要反复执行$\varphi=\varphi \omega_m$,这里的m是当前合并轮次下每个单元的数据规模或者是蝶形运算的步长,$s $ 可以看作是当前合并轮数,$n$是输入规模,$l$是总的轮数。$\omega_m=\omega^{2^{n-s}}$,$s=\log_2m$。一共具有两种预计算方案
方案一: 预计算$\omega$的幂到一个root power表$t$中,即$t[i]=\omega^i ,i\in[0,\frac{n}{2})$。对于给定的$j$和$m=2^s$,我们可以表示旋转因子$\varphi =t[j\cdot 2^{\alpha }], \alpha =n-s,j\in [0,2^{s-1})$。
方案二: 计算每个粒度$s\in[1,n]$,单独的root power表:
$$
T_s[i]=t[i\cdot 2^{n-s}]=(\omega^{2^{n-s}})^i, i\in [0,2^{s-1})
$$
记$T_n=t$,$\sum_{s=1}^n|T_s|=\sum_{s=1}^n 2^{s-1}=2^n-1$。对于给定的$j$和$m=2^s$,我们可以表示旋转因子$\varphi =T[j]$。然后我们将将所有的$T_s$组成一个大的表$T$。
$$
T_s[i]=T[(2^0+2^1+2^2+ \cdots +2^{s-2})+i]=T[2^{s-1}-1+i]
$$
对于给定的$j$和$m=2^s$,我们可以表示旋转因子$\varphi =T[\beta + j],\beta=2^{s-1}-1=\frac{m}{2}-1$。
两种方式$T[\beta+j]$ 和$t[j \cdot 2^\alpha ]$,内层索引都是相同的,$\alpha$ 和 $\beta$表示循环中不变的表达式,在循环开始前计算一次。但是$T$,可以使用指针指向$T[\beta]$,
一步解引用。而$t$需要先位移后解引用。
Four-step算法: 因为要用到所有的幂次,所以直接预计算所有的幂次,构建幂次表$T_*$即可。需要设计合适的索引。我的想法是利用折半引理,在对行或是对列的NTT中索引格式只需要在方案二的基础上进行细微改动即可,只需要乘上总规模$N$除当前NTT规模$n$的商即可,$T_*[(\beta+j)\frac{N}{n}]=T_*[\beta \mu+j\mu]$,只是这种方法会使得方案本一步完成的解引用,需要两步而且增加的是开销较高的乘法。至于列运算结束后的旋转因子矩阵直接按照输入索引去查询即可,因为输入矩阵和旋转因子因子矩阵是一一对应的。
2.3 转置优化
矩阵的转置有两种方式一种是out-place,一种是in-place。前者需要申请一块同等大小的空间,从而完成转置,即空间复杂度$O(R\times C)$。后一种,空间复杂度远小于$O(R\times C)$。这里主要讨论in-place转置方案,对于方阵很简单只需要交换$<i,j>$与$<j,i>$处的元素即可。
下面讨论$n\times cn$形式的矩阵转置,为了方便表示不妨取$c=2$。将一个$n\times 2n$的矩阵$M$拆分成两个$n\times n$的方阵$A$和$B$:
$$
M=[A \quad B]
$$
则转置表达为:
$$
M^T=[A \quad B]^T=
\begin{bmatrix}
A^T\\\
B^T
\end{bmatrix}
$$
定义$\phi(M)$:
$$
\phi(M)=[A^T\quad B^T]
$$
现在将两个子矩阵$A^T$,$B^T$的行用向量表示:
$$
\phi(M)=[A^T\quad B^T]=
\begin{bmatrix}
\alpha_1 & \beta_1\\\
\cdots &\cdots \\\
\alpha_n & \beta_n
\end{bmatrix}
\longleftrightarrow<\alpha_1,\beta_1,\alpha_2,\beta_2,\cdots,\alpha_n,\beta_n >
$$
$$
M^T=
\begin{bmatrix}
A^T\\\
B^T
\end{bmatrix}
=
\begin{bmatrix}
\alpha_1 \\\
\cdots \\\
\alpha_n \\\
\beta_1 \\\
\cdots\\\
\beta_n
\end{bmatrix}
\longleftrightarrow <\alpha_1,\alpha_2,\cdots,\alpha_n,\beta_1,\beta_2,\cdots,\beta_n>
$$
所以我们可以通过某种方法$\rho$重新排列$\phi(M)$的索引,使其等于$M^T=\rho \phi(M)$,对于索引$i$的目标位置$j$满足:
$$
j=\rho (i)=n \cdot (i \bmod 2) + (i / 2) \quad i\in[0,2n)
$$
下面探究对于列排布能否实现同样的作用, 首先我们定义对方阵的行进行索引重排为$\rho_r$,对其列进行索引成排为$\rho_c$。很明显对于一个矩阵A,满足一下关系:
$$
(\rho_cX)^T=\rho_rX^T
$$
我们已经证明:
$$
M^T=\rho_r \phi(M)
$$
现在令$M=\rho_c N$,即可获得:
$$
\rho_r \phi(\rho_cN)=(\rho_cN)^T
$$
$$
\rho_r \phi(\rho_cN)=\rho_r(N)^T
$$
$$
\phi(\rho_cN)=N^T
$$
现在证明对列进行排布同样可以完成相应的操作,只不过要现在哎方阵转置前进行列排布。对列进行排布对那内存更友好,需要$O(2n)$的额外空间。
对于$cn\times n$形式的矩阵,只需要对列执行$\rho^{-1}$然后对方阵转置就行。
2.4 可能的优化
2.4.1 位逆序省略
我们回到最开始,我们引入DFT是为了进行多项式乘法:
$$
A(x)\cdot B(x)=IDFT(DFT(A)\cdot DFT(B))
$$
如果使用$DIF$完成$DFT$,使用$DIT$完成$IDFT$,我们就可以省略$DIF$最后的位逆序,以及$DIT$最开始的位逆序,紧挨着的两个位逆序可以省略。
2.4.2 省略转置
矩阵算法省略转置的原理与位逆序省略的原理相同,如果连续做$DFT$和$IDFT$,我们可以省略$DFT$最后的转置以及$IDFT$最开始的转置。
2.4.3 合并
可以将对列之后乘旋转因子的操作合并到对列操作或者对行操作中,这样可以减少内存读写的次数。
对于$IDFT$可以将乘以$n^{-1}$,合并到四步$IDFT*$中,例如乘旋转因子的过程中。
参考文献
[1]七海. 基础知识:FFT - 简单入门[EB/OL]//七海の参考書. (2021-03-29)[2024-01-21]. https://shiraha.cn/2021/The-concept-of-fft-introducing-edition/ .
[2]快速数论变换(NTT)及蝴蝶操作构造详解[EB/OL]//知乎专栏. [2024-01-21]. https://zhuanlan.zhihu.com/p/80297169 .
[3]Frigo M, Leiserson C E, Prokop H, et al. Cache-oblivious algorithms[J]. ACM Transactions on Algorithms (TALG), 2012, 8(1): 1-22. https://doi.org/10.1145/2071379.2071383 .
[4]LESAVOUREY A, NEGRE C, PLANTARD T. Efficient Randomized Regular Modular Exponentiation using Combined Montgomery and Barrett Multiplications[C/OL]//ICETE: International Joint Conference on e-Business and Telecommunications: 4 [SECRYPT]. Lisbon, Portugal, 2016: 368-375[2024-02-28]. https://hal.science/hal-01330898 . DOI:10.5220/0005998503680375 .
[5]Finite Field Implementations[Z/OL]. [2024-01-26]. https://docs.google.com/presentation/d/1I5QS58LtA3iiiPiVHHcN7oufCoo8sIDh9UvnJHWjA2Q .
[6]RISC ZERO. Finite Field Implementations: Barrett & Montgomery[Z/OL]. (2023-02-17)[2024-01-26]. https://www.youtube.com/watch?v=hUl8ZB6hpUM .
[7]AGARWAL R C, COOLEY J W. Fourier transform and convolution subroutines for the IBM 3090 Vector Facility[J/OL]. IBM Journal of Research and Development, 1986, 30(2): 145-161. DOI:10.1147/rd.302.0145 .
[8]董晓算法. G41 快速傅里叶变换 FFT算法 多项式乘法_哔哩哔哩_bilibili[EB/OL]. [2024-01-21]. https://www.bilibili.com/video/BV1Le4y1V78D/ .
[9]董晓算法. G43 快速数论变换 NTT算法_哔哩哔哩_bilibili[EB/OL]. [2024-01-21]. https://www.bilibili.com/video/BV1a3411Z7vL/ .
[10]HEIDEAN M, JOHNSON D, BURRUS C. Gauss and the history of the fast fourier transform[J/OL]. IEEE ASSP Magazine, 1984, 1(4): 14-21. DOI:10.1109/MASSP.1984.1162257 .
[11]COHEN H, FREY G, AVANZI R, 等. Handbook of Elliptic and Hyperelliptic Curve Cryptography[M/OL]. 0 版. Chapman and Hall/CRC, 2005[2024-02-26]. https://www.taylorfrancis.com/books/9781420034981 . DOI:10.1201/9781420034981 .
[12]Hardcaml Zprize[EB/OL]. [2024-01-30]. https://zprize.hardcaml.com/ntt-top-level.html .
[13]IEEE Xplore Full-Text PDF:[EB/OL]. [2024-02-28]. https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=4176858 .
[14]Math & Engineering[EB/OL]. [2024-02-22]. https://xn–2-umb.com/ .
[15]LIANG Z, ZHAO Y. Number Theoretic Transform and Its Applications in Lattice-based Cryptosystems: A Survey[M/OL]. arXiv, 2022[2024-01-30]. http://arxiv.org/abs/2211.13546 .
[16]KNAUTH C, ADAS B, WHITFIELD D, 等. Practically efficient methods for performing bit-reversed permutation in C++11 on the x86-64 architecture[M/OL]. arXiv, 2017[2024-01-29]. http://arxiv.org/abs/1708.01873 .
[17]DUPAQUIS V, VENELLI A. Redundant Modular Reduction Algorithms[C/OL]//PROUFF E. Smart Card Research and Advanced Applications. Berlin, Heidelberg: Springer, 2011: 102-114. DOI:10.1007/978-3-642-27257-8_7 .
[18]Knezevic M, Vercauteren F, Verbauwhede I. Speeding up Barrett and Montgomery modular multiplications[J]. IEEE Transactions on Comput, 2009, 2.bar_mont.pdf (kuleuven.be)
[19]KRAPIVENSKY V. Speeding up decimal multiplication[M/OL]. arXiv, 2020[2024-01-21]. http://arxiv.org/abs/2011.11524 . DOI:10.48550/arXiv.2011.11524 .
[20]LONGA P, NAEHRIG M. Speeding up the Number Theoretic Transform for Faster Ideal Lattice-Based Cryptography[A/OL]. (2016)[2024-01-30]. https://eprint.iacr.org/2016/504 .
[21]REDUCIBLE. The Fast Fourier Transform (FFT): Most Ingenious Algorithm Ever?[Z/OL]. (2020-11-15)[2024-01-21]. https://www.youtube.com/watch?v=h7apO7q16V0 .